SciPy - 快速指南
SciPy - Introduction
SciPy,发音为Sigh Pi,是一个科学的python开源,分发在BSD许可的库下,用于执行数学,科学和工程计算。
SciPy库依赖于NumPy,它提供方便快捷的N维数组操作。 SciPy库可与NumPy阵列配合使用,并提供许多用户友好且高效的数值实践,例如数值集成和优化的例程。 它们一起运行在所有流行的操作系统上,可以快速安装并且是免费的。 NumPy和SciPy易于使用,但功能强大,足以让一些世界领先的科学家和工程师依赖。
SciPy Sub-packages
SciPy被组织成涵盖不同科学计算领域的子包。 这些总结在下表中 -
| scipy.cluster | 矢量量化/ Kmeans |
| scipy.constants | Physical and mathematical constants |
| scipy.fftpack | Fourier transform |
| scipy.integrate | 集成例程 |
| scipy.interpolate | Interpolation |
| scipy.io | 数据输入和输出 |
| scipy.linalg | Linear algebra routines |
| scipy.ndimage | n-dimensional image package |
| scipy.odr | Orthogonal distance regression |
| scipy.optimize | Optimization |
| scipy.signal | 信号处理 |
| scipy.sparse | 稀疏矩阵 |
| scipy.spatial | 空间数据结构和算法 |
| scipy.special | Any special mathematical functions |
| scipy.stats | Statistics |
数据结构
SciPy使用的基本数据结构是NumPy模块提供的多维数组。 NumPy为线性代数,傅里叶变换和随机数生成提供了一些功能,但没有提供SciPy中等效函数的通用性。
SciPy - Environment Setup
标准Python发行版不与任何SciPy模块捆绑在一起。 轻量级替代方法是使用流行的Python包安装程序安装SciPy,
pip install pandas
如果我们安装Anaconda Python package ,默认情况下将安装Pandas。 以下是在不同操作系统中安装它们的软件包和链接。
Windows
Anaconda (来自https://www.continuum.io )是SciPy堆栈的免费Python发行版。 它也适用于Linux和Mac。
Canopy ( https://www.enthought.com/products/canopy/ )免费提供,以及用于Windows,Linux和Mac的完整SciPy堆栈的商业发行版。
Python (x,y) - 这是一个免费的Python发行版,包含SciPy堆栈和适用于Windows操作系统的Spyder IDE。 (可从https://python-xy.github.io/下载)
Linux
各个Linux发行版的软件包管理器用于在SciPy堆栈中安装一个或多个软件包。
Ubuntu
我们可以使用以下路径在Ubuntu中安装Python。
sudo apt-get install python-numpy python-scipy
python-matplotlibipythonipython-notebook python-pandas python-sympy python-nose
Fedora
我们可以使用以下路径在Fedora中安装Python。
sudo yum install numpyscipy python-matplotlibipython python-pandas
sympy python-nose atlas-devel
SciPy - Basic Functionality
默认情况下,所有NumPy函数都可通过SciPy命名空间使用。 导入SciPy时,无需显式导入NumPy函数。 NumPy的主要目标是同构多维数组。 它是一个元素表(通常是数字),都是相同的类型,由正整数元组索引。 在NumPy中,尺寸称为轴。 axes的数量称为rank 。
现在,让我们修改NumPy中的Vectors和Matrices的基本功能。 由于SciPy建立在NumPy阵列之上,因此必须了解NumPy基础知识。 由于线性代数的大多数部分仅涉及矩阵。
NumPy矢量
可以通过多种方式创建矢量。 其中一些描述如下。
将类似Python数组的对象转换为NumPy
让我们考虑以下示例。
import numpy as np
list = [1,2,3,4]
arr = np.array(list)
print arr
上述程序的输出如下。
[1 2 3 4]
内在的NumPy数组创建
NumPy具有从头开始创建数组的内置函数。 下面解释了其中一些功能。
Using zeros()
零(形状)函数将创建一个填充了具有指定形状的0值的数组。 默认的dtype是float64。 让我们考虑以下示例。
import numpy as np
print np.zeros((2, 3))
上述程序的输出如下。
array([[ 0., 0., 0.],
[ 0., 0., 0.]])
Using ones()
ones(shape)函数将创建一个填充1个值的数组。 在所有其他方面它与零相同。 让我们考虑以下示例。
import numpy as np
print np.ones((2, 3))
上述程序的输出如下。
array([[ 1., 1., 1.],
[ 1., 1., 1.]])
Using arange()
arange()函数将创建具有定期递增值的数组。 让我们考虑以下示例。
import numpy as np
print np.arange(7)
上述程序将生成以下输出。
array([0, 1, 2, 3, 4, 5, 6])
定义值的数据类型
让我们考虑以下示例。
import numpy as np
arr = np.arange(2, 10, dtype = np.float)
print arr
print "Array Data Type :",arr.dtype
上述程序将生成以下输出。
[ 2. 3. 4. 5. 6. 7. 8. 9.]
Array Data Type : float64
Using linspace()
linspace()函数将创建具有指定数量元素的数组,这些元素将在指定的开始值和结束值之间平均间隔。 让我们考虑以下示例。
import numpy as np
print np.linspace(1., 4., 6)
上述程序将生成以下输出。
array([ 1. , 1.6, 2.2, 2.8, 3.4, 4. ])
Matrix
矩阵是一种专用的二维阵列,通过操作保留其二维特性。 它有一些特殊的运算符,如*(矩阵乘法)和**(矩阵幂)。 让我们考虑以下示例。
import numpy as np
print np.matrix('1 2; 3 4')
上述程序将生成以下输出。
matrix([[1, 2],
[3, 4]])
矩阵的共轭转置
此功能返回self的(复杂)共轭转置。 让我们考虑以下示例。
import numpy as np
mat = np.matrix('1 2; 3 4')
print mat.H
上述程序将生成以下输出。
matrix([[1, 3],
[2, 4]])
矩阵的转置
此功能返回self的转置。 让我们考虑以下示例。
import numpy as np
mat = np.matrix('1 2; 3 4')
mat.T
上述程序将生成以下输出。
matrix([[1, 3],
[2, 4]])
当我们转置矩阵时,我们创建一个新的矩阵,其行是原始的列。 另一方面,共轭转置为每个矩阵元素交换行和列索引。 矩阵的逆是矩阵,如果与原始矩阵相乘,则得到单位矩阵。
SciPy - Cluster
K-means clustering是一种在一组未标记数据中查找聚类和聚类中心的方法。 直觉上,我们可能会认为一个聚类是由一组数据点组成的,它们的点间距离与到聚类外部点的距离相比较小。 给定一组初始的K中心,K-means算法迭代以下两个步骤 -
对于每个中心,识别比其更靠近它的训练点子集(其簇)比任何其他中心。
计算每个聚类中数据点的每个特征的平均值,并且该平均向量成为该聚类的新中心。
迭代这两个步骤直到中心不再移动或分配不再改变。 然后,可以将新点x分配给最近原型的簇。 SciPy库通过集群包提供了良好的K-Means算法实现。 让我们了解如何使用它。
K-Means在SciPy中的实现
我们将了解如何在SciPy中实现K-Means。
Import K-Means
我们将看到每个导入函数的实现和使用。
from SciPy.cluster.vq import kmeans,vq,whiten
数据生成
我们必须模拟一些数据来探索聚类。
from numpy import vstack,array
from numpy.random import rand
# data generation with three features
data = vstack((rand(100,3) + array([.5,.5,.5]),rand(100,3)))
现在,我们必须检查数据。 上述程序将生成以下输出。
array([[ 1.48598868e+00, 8.17445796e-01, 1.00834051e+00],
[ 8.45299768e-01, 1.35450732e+00, 8.66323621e-01],
[ 1.27725864e+00, 1.00622682e+00, 8.43735610e-01],
…………….
基于每个特征标准化一组观察。 在运行K-Means之前,通过美白重新调整观察集的每个特征维度是有益的。 每个特征除以所有观测值的标准偏差,以给出单位方差。
美白数据
我们必须使用以下代码来白化数据。
# whitening of data
data = whiten(data)
用三个集群计算K-Means
现在让我们使用以下代码计算具有三个簇的K-Means。
# computing K-Means with K = 3 (2 clusters)
centroids,_ = kmeans(data,3)
上述代码对形成K个簇的一组观察向量执行K-Means。 K-Means算法调整质心,直到不能进行足够的进展,即失真的变化,因为最后一次迭代小于某个阈值。 在这里,我们可以通过使用下面给出的代码打印质心变量来观察聚类的质心。
print(centroids)
上面的代码将生成以下输出。
print(centroids)[ [ 2.26034702 1.43924335 1.3697022 ]
[ 2.63788572 2.81446462 2.85163854]
[ 0.73507256 1.30801855 1.44477558] ]
使用下面给出的代码将每个值分配给集群。
# assign each sample to a cluster
clx,_ = vq(data,centroids)
vq函数将'M'中的每个观察向量与' obs数组与质心进行比较,并将观测值分配给最近的聚类。 它返回每个观察的簇和失真。 我们也可以检查失真。 让我们使用以下代码检查每个观察的集群。
# check clusters of observation
print clx
上面的代码将生成以下输出。
array([1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 2, 0, 2, 0, 1, 1, 1,
0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0,
0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 0, 0,
2, 2, 2, 1, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2], dtype=int32)
上述阵列的不同值0,1,2表示簇。
SciPy - Constants
SciPy常量包提供了广泛的常量,用于一般科学领域。
SciPy常量包
scipy.constants package提供了各种常量。 我们必须导入所需的常量并根据要求使用它们。 让我们看看如何导入和使用这些常量变量。
首先,让我们通过考虑以下示例来比较'pi'值。
#Import pi constant from both the packages
from scipy.constants import pi
from math import pi
print("sciPy - pi = %.16f"%scipy.constants.pi)
print("math - pi = %.16f"%math.pi)
上述程序将生成以下输出。
sciPy - pi = 3.1415926535897931
math - pi = 3.1415926535897931
可用常量列表
下表简要描述了各种常量。
数学常数
| Sr. No. | 不变 | 描述 |
|---|---|---|
| 1 | pi | pi |
| 2 | golden | Golden Ratio |
物理常数
下表列出了最常用的物理常量。
| Sr. No. | 常量和描述 |
|---|---|
| 1 | c 真空中的光速 |
| 2 | speed_of_light 真空中的光速 |
| 3 | h 普朗克常数 |
| 4 | Planck 普朗克常数h |
| 5 | G 牛顿的引力常数 |
| 6 | e 小学费 |
| 7 | R 摩尔气体常数 |
| 8 | Avogadro 阿伏加德罗不变 |
| 9 | k 玻尔兹曼常数 |
| 10 | electron_mass(OR) m_e 电子质量 |
| 11 | proton_mass (OR) m_p 质子质量 |
| 12 | neutron_mass(OR)m_n 中子质量 |
Units
下表列出了SI单位。
| Sr. No. | 单元 | 值 |
|---|---|---|
| 1 | milli | 0.001 |
| 2 | micro | 1e-06 |
| 3 | kilo | 1000 |
这些单位包括yotta,zetta,exa,peta,tera ...... kilo,hector,... nano,pico,...到zepto。
其他重要的常数
下表列出了SciPy中使用的其他重要常量。
| Sr. No. | 单元 | 值 |
|---|---|---|
| 1 | gram | 0.001 kg |
| 2 | 原子量 | Atomic mass constant |
| 3 | degree | Degree in radians |
| 4 | minute | 一秒钟一分钟 |
| 5 | day | One day in seconds |
| 6 | inch | 一英寸米 |
| 7 | micron | 一米多米 |
| 8 | light_year | 一米一米 |
| 9 | atm | Standard atmosphere in pascals |
| 10 | acre | 一英亩平方米 |
| 11 | liter | 一升立方米 |
| 12 | gallon | 一加仑立方米 |
| 13 | kmh | 每小时公里数,以米/秒为单位 |
| 14 | degree_Fahrenheit | One Fahrenheit in kelvins |
| 15 | eV | 一焦耳电子伏特 |
| 16 | hp | One horsepower in watts |
| 17 | dyn | One dyne in newtons |
| 18 | lambda2nu | 将波长转换为光频率 |
记住所有这些都有点困难。 使用scipy.constants.find()方法获取哪个键的简单方法是哪个函数。 让我们考虑以下示例。
import scipy.constants
res = scipy.constants.physical_constants["alpha particle mass"]
print res
上述程序将生成以下输出。
[
'alpha particle mass',
'alpha particle mass energy equivalent',
'alpha particle mass energy equivalent in MeV',
'alpha particle mass in u',
'electron to alpha particle mass ratio'
]
此方法返回键列表,如果关键字不匹配,则返回任何内容。
SciPy - FFTpack
在时域信号上计算Fourier Transformation以检查其在频域中的行为。 傅里叶变换在信号和噪声处理,图像处理,音频信号处理等学科中得到应用.SciPy提供了fftpack模块,可以让用户计算快速傅里叶变换。
以下是正弦函数的示例,该函数将用于使用fftpack模块计算傅里叶变换。
快速傅里叶变换
让我们详细了解快速傅立叶变换。
一维离散傅立叶变换
通过fft()计算长度N序列x [n]的长度N的FFT y [k],并且使用ifft()计算逆变换。 让我们考虑以下示例
#Importing the fft and inverse fft functions from fftpackage
from scipy.fftpack import fft
#create an array with random n numbers
x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
#Applying the fft function
y = fft(x)
print y
上述程序将生成以下输出。
[ 4.50000000+0.j 2.08155948-1.65109876j -1.83155948+1.60822041j
-1.83155948-1.60822041j 2.08155948+1.65109876j ]
让我们看另一个例子
#FFT is already in the workspace, using the same workspace to for inverse transform
yinv = ifft(y)
print yinv
上述程序将生成以下输出。
[ 1.0+0.j 2.0+0.j 1.0+0.j -1.0+0.j 1.5+0.j ]
scipy.fftpack模块允许计算快速傅里叶变换。 作为说明,(嘈杂的)输入信号可能如下所示 -
import numpy as np
time_step = 0.02
period = 5.
time_vec = np.arange(0, 20, time_step)
sig = np.sin(2 * np.pi/period * time_vec) + 0.5 *np.random.randn(time_vec.size)
print sig.size
我们正在创建一个时间步长为0.02秒的信号。 最后一个语句打印信号sig的大小。 输出如下 -
1000
我们不知道信号频率; 我们只知道信号sig的采样时间步长。 该信号应该来自实函数,因此傅立叶变换将是对称的。 scipy.fftpack.fftfreq()函数将生成采样频率, scipy.fftpack.fft()将计算快速傅立叶变换。
让我们借助一个例子来理解这一点。
from scipy import fftpack
sample_freq = fftpack.fftfreq(sig.size, d = time_step)
sig_fft = fftpack.fft(sig)
print sig_fft
上述程序将生成以下输出。
array([
25.45122234 +0.00000000e+00j, 6.29800973 +2.20269471e+00j,
11.52137858 -2.00515732e+01j, 1.08111300 +1.35488579e+01j,
…….])
离散余弦变换
Discrete Cosine Transform (DCT)根据在不同频率振荡的余弦函数之和来表示有限的数据点序列。 SciPy提供具有功能dct的DCT和具有功能idct的相应IDCT。 让我们考虑以下示例。
from scipy.fftpack import dct
print dct(np.array([4., 3., 5., 10., 5., 3.]))
上述程序将生成以下输出。
array([ 60., -3.48476592, -13.85640646, 11.3137085, 6., -6.31319305])
逆离散余弦变换从其离散余弦变换(DCT)系数重建序列。 idct函数是dct函数的反函数。 让我们通过以下示例来理解这一点。
from scipy.fftpack import dct
print idct(np.array([4., 3., 5., 10., 5., 3.]))
上述程序将生成以下输出。
array([ 39.15085889, -20.14213562, -6.45392043, 7.13341236,
8.14213562, -3.83035081])
SciPy - Integrate
当一个函数不能被分析地集成,或者很难通过分析整合时,人们通常会转向数值积分方法。 SciPy有许多用于执行数值积分的例程。 其中大多数都在同一个scipy.integrate库中找到。 下表列出了一些常用功能。
| 高级编号 | 功能说明 |
|---|---|
| 1 | quad 单一集成 |
| 2 | dblquad 双重整合 |
| 3 | tplquad 三重整合 |
| 4 | nquad n倍多重整合 |
| 5 | fixed_quad 高斯正交,阶数n |
| 6 | quadrature 高斯求积公差 |
| 7 | romberg Romberg整合 |
| 8 | trapz 梯形规则 |
| 9 | cumtrapz 梯形规则累积计算积分 |
| 10 | simps 辛普森的统治 |
| 11 | romb Romberg整合 |
| 12 | polyint 解析多项式积分(NumPy) |
| 13 | poly1d polyint的辅助函数(NumPy) |
单积分
Quad功能是SciPy集成功能的主力。 数值积分有时被称为quadrature ,因此得名。 它通常是在a到b的给定固定范围内执行函数f(x)单积分的默认选择。
$$\int_{a}^{b} f(x)dx$$
quad的一般形式是scipy.integrate.quad(f, a, b) ,其中'f'是要集成的函数的名称。 然而,'a'和'b'分别是下限和上限。 让我们看一下高斯函数的一个例子,它集成在0和1的范围内。
我们首先需要定义函数→$ f(x)= e ^ { - x ^ 2} $,这可以使用lambda表达式完成,然后在该函数上调用quad方法。
import scipy.integrate
from numpy import exp
f= lambda x:exp(-x**2)
i = scipy.integrate.quad(f, 0, 1)
print i
上述程序将生成以下输出。
(0.7468241328124271, 8.291413475940725e-15)
quad函数返回两个值,其中第一个数字是积分值,第二个值是积分值中绝对误差的估计值。
Note - 由于quad需要函数作为第一个参数,我们不能直接将exp作为参数传递。 Quad函数接受正无穷大作为限制。 Quad函数可以集成单个变量的标准预定义NumPy函数,例如exp,sin和cos。
多重积分
双重和三重集成的机制已经包含在函数dblquad, tplquad和nquad 。 这些函数分别集成了四个或六个参数。 所有内积分的极限需要定义为函数。
双积分
dblquad的一般形式是scipy.integrate.dblquad(func,a,b,gfun,hfun)。 其中,func是要集成的函数的名称,'a'和'b'分别是x变量的下限和上限,而gfun和hfun是定义下限和上限的函数的名称。的变量。
举个例子,让我们执行双积分方法。
$$\int_{0}^{1/2} dy \int_{0}^{\sqrt{1-4y^2}} 16xy \:dx$$
我们使用lambda表达式定义函数f,g和h。 请注意,即使g和h是常量,因为它们可能在很多情况下,它们必须被定义为函数,正如我们在这里为下限所做的那样。
import scipy.integrate
from numpy import exp
from math import sqrt
f = lambda x, y : 16*x*y
g = lambda x : 0
h = lambda y : sqrt(1-4*y**2)
i = scipy.integrate.dblquad(f, 0, 0.5, g, h)
print i
上述程序将生成以下输出。
(0.5, 1.7092350012594845e-14)
除了上面描述的例程之外,scipy.integrate还有许多其他集成例程,包括执行n倍多重集成的nquad,以及实现各种集成算法的其他例程。 但是,quad和dblquad将满足我们对数值积分的大部分需求。
SciPy - Interpolate
在本章中,我们将讨论插值如何帮助SciPy。
什么是插值?
插值是在线或曲线上的两个点之间找到值的过程。 为了帮助我们记住它意味着什么,我们应该想到“inter”这个词的第一部分,意思是“输入”,这提醒我们要看看我们原来拥有的数据“内部”。 此工具插值不仅在统计学中有用,而且在科学,商业或需要预测属于两个现有数据点的值时也很有用。
让我们创建一些数据,看看如何使用scipy.interpolate包完成插值。
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.linspace(0, 4, 12)
y = np.cos(x**2/3+4)
print x,y
上述程序将生成以下输出。
(
array([0., 0.36363636, 0.72727273, 1.09090909, 1.45454545, 1.81818182,
2.18181818, 2.54545455, 2.90909091, 3.27272727, 3.63636364, 4.]),
array([-0.65364362, -0.61966189, -0.51077021, -0.31047698, -0.00715476,
0.37976236, 0.76715099, 0.99239518, 0.85886263, 0.27994201,
-0.52586509, -0.99582185])
)
现在,我们有两个数组。 假设这两个数组是空间中点的两个维度,让我们使用以下程序进行绘图,看看它们的外观。
plt.plot(x, y,’o’)
plt.show()
上述程序将生成以下输出。

1-D Interpolation
scipy.interpolate中的interp1d类是一种基于固定数据点创建函数的便捷方法,可以使用线性插值在给定数据定义的域内的任何位置进行求值。
通过使用上述数据,让我们创建一个插值函数并绘制一个新的插值图。
f1 = interp1d(x, y,kind = 'linear')
f2 = interp1d(x, y, kind = 'cubic')
使用interp1d函数,我们创建了两个函数f1和f2。 对于给定的输入x,这些函数返回y。 第三种变量类型表示插值技术的类型。 '线性','最近','零','线性','二次','立方'是一些插值技术。
现在,让我们创建一个更长的新输入,以查看插值的明显差异。 我们将在新数据上使用旧数据的相同功能。
xnew = np.linspace(0, 4,30)
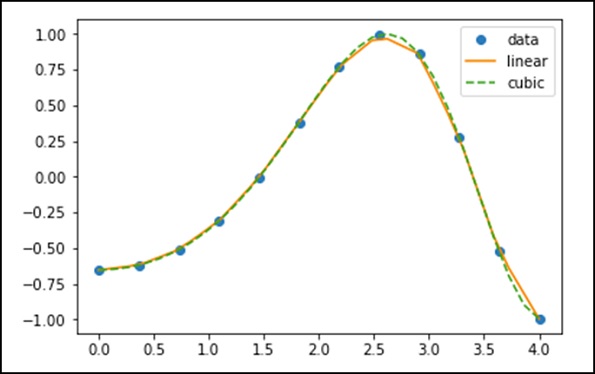
plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
plt.legend(['data', 'linear', 'cubic','nearest'], loc = 'best')
plt.show()
上述程序将生成以下输出。
Splines
为了通过数据点绘制平滑的曲线,起草人曾使用过薄的柔性木条,硬橡胶,金属或塑料称为机械花键。 为了使用机械花键,在设计中沿着曲线明智地选择销钉,然后弯曲花键,使其接触这些销钉中的每一个。
显然,采用这种结构,样条曲线在这些引脚处插入曲线。 它可用于在其他图纸中重现曲线。 引脚所在的点称为结。 我们可以通过调整节点的位置来更改样条曲线定义的曲线的形状。
单变量样条
一维平滑样条拟合一组给定的数据点。 scipy.interpolate中的UnivariateSpline类是基于固定数据点类创建函数的便捷方法 - scipy.interpolate.UnivariateSpline(x,y,w = None,bbox = [None,None],k = 3,s =无,ext = 0,check_finite = False)。
Parameters - 以下是单变量样条曲线的参数。
这使得度数k的样条y = spl(x)与提供的x,y数据拟合。
'w' - 指定样条拟合的权重。 必须是积极的。 如果没有(默认),权重都是相等的。
's' - 通过指定平滑条件指定结的数量。
'k' - 平滑样条曲线的度数。 必须<= 5.默认值为k = 3,三次样条曲线。
Ext - 控制不在结节序列定义的区间内的元素的外推模式。
如果ext = 0或'extrapolate',则返回外推值。
如果ext = 1或'0',则返回0
如果ext = 2或'raise',则引发ValueError
如果ext = 3'const',则返回边界值。
check_finite - 是否检查输入数组是否仅包含有限数字。
让我们考虑以下示例。
import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
x = np.linspace(-3, 3, 50)
y = np.exp(-x**2) + 0.1 * np.random.randn(50)
plt.plot(x, y, 'ro', ms = 5)
plt.show()
使用平滑参数的默认值。
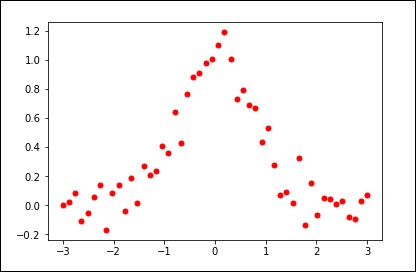
spl = UnivariateSpline(x, y)
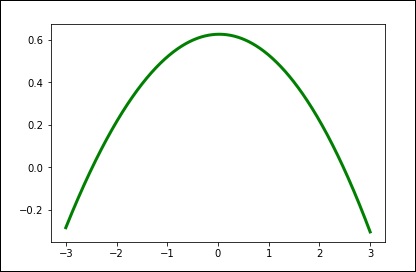
xs = np.linspace(-3, 3, 1000)
plt.plot(xs, spl(xs), 'g', lw = 3)
plt.show()
手动更改平滑量。
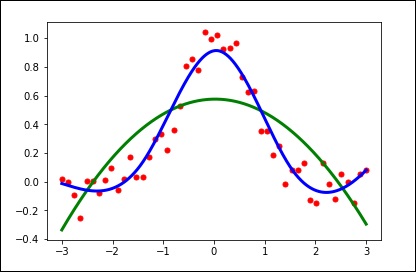
spl.set_smoothing_factor(0.5)
plt.plot(xs, spl(xs), 'b', lw = 3)
plt.show()
SciPy - Input & Output
Scipy.io(输入和输出)包提供了广泛的功能,可以处理不同格式的文件。 其中一些格式是 -
- Matlab
- IDL
- Matrix Market
- Wave
- Arff
- Netcdf, etc.
让我们详细讨论最常用的文件格式 -
MATLAB
以下是用于加载和保存.mat文件的函数。
| Sr. No. | 功能说明 |
|---|---|
| 1 | loadmat 加载MATLAB文件 |
| 2 | savemat 保存MATLAB文件 |
| 3 | whosmat 列出MATLAB文件中的变量 |
让我们考虑以下示例。
import scipy.io as sio
import numpy as np
#Save a mat file
vect = np.arange(10)
sio.savemat('array.mat', {'vect':vect})
#Now Load the File
mat_file_content = sio.loadmat(‘array.mat’)
Print mat_file_content
上述程序将生成以下输出。
{
'vect': array([[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]), '__version__': '1.0',
'__header__': 'MATLAB 5.0 MAT-file Platform: posix, Created on: Sat Sep 30
09:49:32 2017', '__globals__': []
}
我们可以看到数组以及Meta信息。 如果我们想要在不将数据读入内存的情况下检查MATLAB文件的内容,请使用whosmat command ,如下所示。
import scipy.io as sio
mat_file_content = sio.whosmat(‘array.mat’)
print mat_file_content
上述程序将生成以下输出。
[('vect', (1, 10), 'int64')]
SciPy - Linalg
SciPy使用优化的ATLAS LAPACK和BLAS库构建。 它具有非常快速的线性代数功能。 所有这些线性代数例程都期望一个可以转换为二维数组的对象。 这些例程的输出也是二维数组。
SciPy.linalg与NumPy.linalg
scipy.linalg包含numpy.linalg中的所有函数。 另外,scipy.linalg还有一些不在numpy.linalg中的高级函数。 使用scipy.linalg而不是numpy.linalg的另一个好处是它总是使用BLAS/LAPACK支持进行编译,而对于NumPy,这是可选的。 因此,SciPy版本可能会更快,具体取决于NumPy的安装方式。
线性方程组
对于未知的x,y值, scipy.linalg.solve特征求解线性方程a * x + b * y = Z.
作为示例,假设期望解决以下联立方程。
x + 3y + 5z = 10
2x + 5y + z = 8
2x + 3y + 8z = 3
为了求解x,y,z值的上述等式,我们可以使用矩阵求逆找到解向量,如下所示。
$$\begin{bmatrix} x\\ y\\ z \end{bmatrix} = \begin{bmatrix} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8 \end{bmatrix}^{-1} \begin{bmatrix} 10\\ 8\\ 3 \end{bmatrix} = \frac{1}{25} \begin{bmatrix} -232\\ 129\\ 19 \end{bmatrix} = \begin{bmatrix} -9.28\\ 5.16\\ 0.76 \end{bmatrix}.$$
但是,最好使用linalg.solve命令,它可以更快,更稳定。
求解函数采用两个输入'a'和'b',其中'a'表示系数,'b'表示相应的右手侧值并返回解数组。
让我们考虑以下示例。
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy arrays
a = np.array([[3, 2, 0], [1, -1, 0], [0, 5, 1]])
b = np.array([2, 4, -1])
#Passing the values to the solve function
x = linalg.solve(a, b)
#printing the result array
print x
上述程序将生成以下输出。
array([ 2., -2., 9.])
寻找决定因素
方阵A的行列式通常表示为| A | 并且是线性代数中经常使用的量。 在SciPy中,这是使用det()函数计算的。 它将矩阵作为输入并返回标量值。
让我们考虑以下示例。
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
A = np.array([[1,2],[3,4]])
#Passing the values to the det function
x = linalg.det(A)
#printing the result
print x
上述程序将生成以下输出。
-2.0
特征值和特征向量
特征值 - 特征向量问题是最常用的线性代数运算之一。 通过考虑以下关系,我们可以找到方形矩阵(A)的特征值(λ)和相应的特征向量(v) -
Av = λv
scipy.linalg.eig根据普通或广义特征值问题计算特征值。 该函数返回特征值和特征向量。
让我们考虑以下示例。
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
A = np.array([[1,2],[3,4]])
#Passing the values to the eig function
l, v = linalg.eig(A)
#printing the result for eigen values
print l
#printing the result for eigen vectors
print v
上述程序将生成以下输出。
array([-0.37228132+0.j, 5.37228132+0.j]) #--Eigen Values
array([[-0.82456484, -0.41597356], #--Eigen Vectors
[ 0.56576746, -0.90937671]])
奇异值分解
奇异值分解(SVD)可以被认为是特征值问题对非平方矩阵的扩展。
scipy.linalg.svd将矩阵'a'分解为两个酉矩阵'U'和'Vh'以及一个奇异值(真实,非负)的1-D数组',使得a == U * S * Vh,其中'S'是一个适当形状的零矩阵,主对角线's'。
让我们考虑以下示例。
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
a = np.random.randn(3, 2) + 1.j*np.random.randn(3, 2)
#Passing the values to the eig function
U, s, Vh = linalg.svd(a)
# printing the result
print U, Vh, s
上述程序将生成以下输出。
(
array([
[ 0.54828424-0.23329795j, -0.38465728+0.01566714j,
-0.18764355+0.67936712j],
[-0.27123194-0.5327436j , -0.57080163-0.00266155j,
-0.39868941-0.39729416j],
[ 0.34443818+0.4110186j , -0.47972716+0.54390586j,
0.25028608-0.35186815j]
]),
array([ 3.25745379, 1.16150607]),
array([
[-0.35312444+0.j , 0.32400401+0.87768134j],
[-0.93557636+0.j , -0.12229224-0.33127251j]
])
)
SciPy - Ndimage
SciPy ndimage子模块专用于图像处理。 这里,ndimage意味着n维图像。
图像处理中一些最常见的任务如下&miuns;
- 输入/输出,显示图像
- 基本操作 - 裁剪,翻转,旋转等
- 图像过滤 - 去噪,锐化等
- 图像分割 - 标记与不同对象相对应的像素
- Classification
- Feature extraction
- Registration
让我们讨论如何使用SciPy实现其中一些。
打开和写入图像文件
SciPy中的misc package带有一些图像。 我们使用这些图像来学习图像处理。 让我们考虑以下示例。
from scipy import misc
f = misc.face()
misc.imsave('face.png', f) # uses the Image module (PIL)
import matplotlib.pyplot as plt
plt.imshow(f)
plt.show()
上述程序将生成以下输出。

原始格式的任何图像都是由矩阵格式中的数字表示的颜色组合。 机器仅基于这些数字理解和操纵图像。 RGB是一种流行的表现方式。
让我们看看上面图像的统计信息。
from scipy import misc
face = misc.face(gray = False)
print face.mean(), face.max(), face.min()
上述程序将生成以下输出。
110.16274388631184, 255, 0
现在,我们知道图像是由数字组成的,因此数字值的任何变化都会改变原始图像。 让我们对图像进行一些几何变换。 基本的几何操作是裁剪
from scipy import misc
face = misc.face(gray = True)
lx, ly = face.shape
# Cropping
crop_face = face[lx/4: - lx/4, ly/4: - ly/4]
import matplotlib.pyplot as plt
plt.imshow(crop_face)
plt.show()
上述程序将生成以下输出。
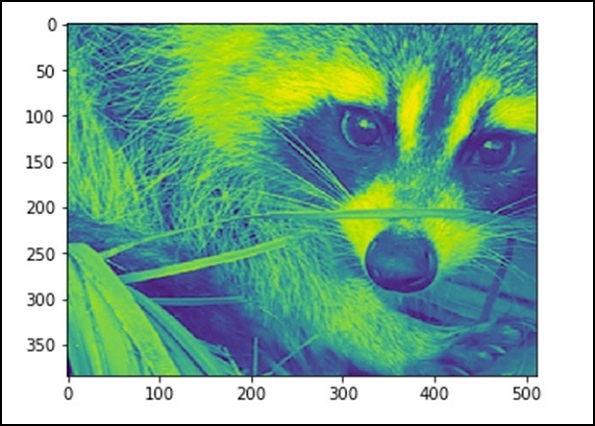
我们还可以执行一些基本操作,例如将图像颠倒,如下所述。
# up <-> down flip
from scipy import misc
face = misc.face()
flip_ud_face = np.flipud(face)
import matplotlib.pyplot as plt
plt.imshow(flip_ud_face)
plt.show()
上述程序将生成以下输出。

除此之外,我们还有rotate() function ,它以指定的角度旋转图像。
# rotation
from scipy import misc,ndimage
face = misc.face()
rotate_face = ndimage.rotate(face, 45)
import matplotlib.pyplot as plt
plt.imshow(rotate_face)
plt.show()
上述程序将生成以下输出。
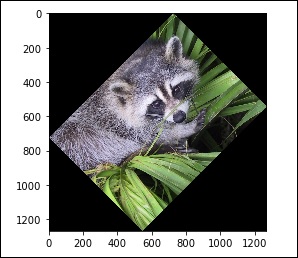
过滤器 (Filters)
让我们讨论过滤器如何帮助图像处理。
什么是图像处理中的过滤?
过滤是一种用于修改或增强图像的技术。 例如,您可以过滤图像以强调某些功能或删除其他功能。 通过过滤实现的图像处理操作包括平滑,锐化和边缘增强。
滤波是邻域操作,其中通过将一些算法应用于相应输入像素的邻域中的像素的值来确定输出图像中的任何给定像素的值。 现在让我们使用SciPy ndimage执行一些操作。
Blurring
模糊被广泛用于降低图像中的噪声。 我们可以执行过滤操作并查看图像中的变化。 让我们考虑以下示例。
from scipy import misc
face = misc.face()
blurred_face = ndimage.gaussian_filter(face, sigma=3)
import matplotlib.pyplot as plt
plt.imshow(blurred_face)
plt.show()
上述程序将生成以下输出。

西格玛值表示五个等级的模糊程度。 我们可以通过调整sigma值来查看图像质量的变化。 有关模糊的更多详细信息,请单击→DIP(数字图像处理)教程。
边缘检测
让我们讨论边缘检测如何帮助图像处理。
什么是边缘检测?
边缘检测是一种用于查找图像内对象边界的图像处理技术。 它的工作原理是检测亮度的不连续性。 边缘检测用于图像处理,计算机视觉和机器视觉等领域的图像分割和数据提取。
最常用的边缘检测算法包括
- Sobel
- Canny
- Prewitt
- Roberts
- Fuzzy Logic methods
让我们考虑以下示例。
import scipy.ndimage as nd
import numpy as np
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im[90:-90,90:-90] = 2
im = ndimage.gaussian_filter(im, 8)
import matplotlib.pyplot as plt
plt.imshow(im)
plt.show()
上述程序将生成以下输出。
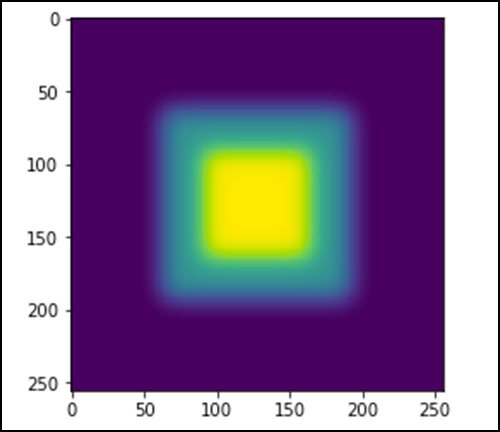
图像看起来像一个方块的颜色。 现在,我们将检测那些彩色块的边缘。 这里,ndimage提供了一个名为Sobel的函数来执行此操作。 然而,NumPy提供了Hypot函数来将两个结果矩阵组合成一个。
让我们考虑以下示例。
import scipy.ndimage as nd
import matplotlib.pyplot as plt
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im[90:-90,90:-90] = 2
im = ndimage.gaussian_filter(im, 8)
sx = ndimage.sobel(im, axis = 0, mode = 'constant')
sy = ndimage.sobel(im, axis = 1, mode = 'constant')
sob = np.hypot(sx, sy)
plt.imshow(sob)
plt.show()
上述程序将生成以下输出。
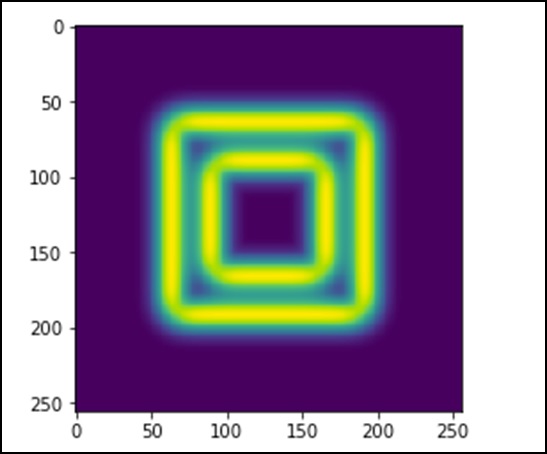
SciPy - Optimize
scipy.optimize package提供了几种常用的优化算法。 该模块包含以下几个方面 -
使用各种算法(例如BFGS,Nelder-Mead simplex,Newton Conjugate Gradient,COBYLA或SLSQP)对多变量标量函数(最小化())进行无约束和约束最小化
全局(强力)优化程序(例如,退火(),流域购物())
最小二乘最小化(leastsq())和曲线拟合(curve_fit())算法
标量单变量函数最小化器(minimize_scalar())和根查找器(newton())
使用各种算法的多变量方程系统求解器(root())(例如混合Powell,Levenberg-Marquardt或大规模方法,如Newton-Krylov)
无约束和约束最小化多元标量函数
minimize() function为scipy.optimize多变量标量函数提供了无约束和约束最小化算法的通用接口。 为了演示最小化函数,考虑最小化NN变量的Rosenbrock函数的问题 -
$$f(x) = \sum_{i = 1}^{N-1} \:100(x_i - x_{i-1}^{2})$$
该函数的最小值为0,这是在xi = 1时实现的。
Nelder-Mead单纯形算法
在以下示例中,minimize()例程与Nelder-Mead simplex algorithm (method = 'Nelder-Mead') (通过方法参数选择)。 让我们考虑以下示例。
import numpy as np
from scipy.optimize import minimize
def rosen(x):
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(rosen, x0, method='nelder-mead')
print(res.x)
上述程序将生成以下输出。
[7.93700741e+54 -5.41692163e+53 6.28769150e+53 1.38050484e+55 -4.14751333e+54]
单纯形算法可能是最简化一个相当良好的函数的最简单方法。 它只需要功能评估,是简单最小化问题的理想选择。 但是,由于它不使用任何梯度评估,因此可能需要更长时间才能找到最小值。
另一种只需要函数调用来找到最小值的优化算法是Powell's method ,可以通过在minimize()函数中设置method ='powell'来实现。
最小二乘
求解带变量边界的非线性最小二乘问题。 给定残差f(x)(n个实数变量的m维实函数)和损失函数rho(s)(标量函数),least_squares找到代价函数F(x)的局部最小值。 让我们考虑以下示例。
在这个例子中,我们找到了Rosenbrock函数的最小值,而没有自变量的界限。
#Rosenbrock Function
def fun_rosenbrock(x):
return np.array([10 * (x[1] - x[0]**2), (1 - x[0])])
from scipy.optimize import least_squares
input = np.array([2, 2])
res = least_squares(fun_rosenbrock, input)
print res
请注意,我们只提供残差的向量。 该算法将成本函数构造为残差的平方和,得到Rosenbrock函数。 确切的最小值是x = [1.0,1.0]。
上述程序将生成以下输出。
active_mask: array([ 0., 0.])
cost: 9.8669242910846867e-30
fun: array([ 4.44089210e-15, 1.11022302e-16])
grad: array([ -8.89288649e-14, 4.44089210e-14])
jac: array([[-20.00000015,10.],[ -1.,0.]])
message: '`gtol` termination condition is satisfied.'
nfev: 3
njev: 3
optimality: 8.8928864934219529e-14
status: 1
success: True
x: array([ 1., 1.])
找根
让我们了解根发现如何帮助SciPy。
Scalar 函数
如果有一个单变量方程,则可以尝试四种不同的根寻找算法。 这些算法中的每一个都需要预期根的间隔的端点(因为函数改变了符号)。 一般来说, brentq是最佳选择,但其他方法在某些情况下或出于学术目的可能有用。
Fixed-point solving
与找到函数的零密切相关的问题是找到函数的固定点的问题。 函数的固定点是函数的求值返回点的点:g(x)= x。 显然, gg的固定点是f(x)= g(x)-x的根。 等价地, ff的根是g(x)= f(x)+ x的fixed_point。 例程fixed_point提供了一个简单的迭代方法,使用Aitkens sequence acceleration来估计gg的固定点,如果给出了起始点。
方程组
使用root() function可以找到一组非线性方程的root() function 。 有几种方法可供选择,其中hybr (默认)和lm分别使用hybrid method of Powell的hybrid method of Powell和MINPACK的Levenberg-Marquardt method 。
以下示例考虑单变量超越方程。
x 2 + 2cos(x) = 0
其根可以找到如下 -
import numpy as np
from scipy.optimize import root
def func(x):
return x*2 + 2 * np.cos(x)
sol = root(func, 0.3)
print sol
上述程序将生成以下输出。
fjac: array([[-1.]])
fun: array([ 2.22044605e-16])
message: 'The solution converged.'
nfev: 10
qtf: array([ -2.77644574e-12])
r: array([-3.34722409])
status: 1
success: True
x: array([-0.73908513])
SciPy - Stats
所有统计函数都位于子包scipy.stats并且可以使用info(stats)函数获得这些函数的相当完整的列表。 还可以从stats子包的docstring获取可用随机变量列表。 该模块包含大量概率分布以及不断增长的统计函数库。
每个单变量分布都有自己的子类,如下表所述 -
| Sr. No. | 类和描述 |
|---|---|
| 1 | rv_continuous 一个通用的连续随机变量类,用于子类化 |
| 2 | rv_discrete 通用的离散随机变量类,用于子类化 |
| 3 | rv_histogram 生成直方图给出的分布 |
正常连续随机变量
随机变量X可以取任何值的概率分布是连续随机变量。 location(loc)关键字指定平均值。 scale(scale)关键字指定标准偏差。
作为rv_continuous类的一个实例, norm对象从它继承了泛型方法的集合,并使用特定于此特定分布的详细信息完成它们。
要在多个点计算CDF,我们可以传递列表或NumPy数组。 让我们考虑以下示例。
from scipy.stats import norm
import numpy as np
print norm.cdf(np.array([1,-1., 0, 1, 3, 4, -2, 6]))
上述程序将生成以下输出。
array([ 0.84134475, 0.15865525, 0.5 , 0.84134475, 0.9986501 ,
0.99996833, 0.02275013, 1. ])
为了找到分布的中值,我们可以使用百分点函数(PPF),它是CDF的倒数。 让我们通过使用以下示例来理解。
from scipy.stats import norm
print norm.ppf(0.5)
上述程序将生成以下输出。
0.0
要生成随机变量序列,我们应该使用size关键字参数,如下例所示。
from scipy.stats import norm
print norm.rvs(size = 5)
上述程序将生成以下输出。
array([ 0.20929928, -1.91049255, 0.41264672, -0.7135557 , -0.03833048])
以上输出不可再现。 要生成相同的随机数,请使用种子函数。
统一分配
可以使用均匀函数生成均匀分布。 让我们考虑以下示例。
from scipy.stats import uniform
print uniform.cdf([0, 1, 2, 3, 4, 5], loc = 1, scale = 4)
上述程序将生成以下输出。
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])
建立离散分布
让我们生成一个随机样本,并将观察到的频率与概率进行比较。
二项分布
作为rv_discrete class一个实例, binom object从它继承了泛型方法的集合,并使用特定于此特定分发的详细信息完成它们。 让我们考虑以下示例。
from scipy.stats import uniform
print uniform.cdf([0, 1, 2, 3, 4, 5], loc = 1, scale = 4)
上述程序将生成以下输出。
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])
描述性统计
Min,Max,Mean和Variance等基本统计信息将NumPy数组作为输入并返回相应的结果。 scipy.stats package中提供的一些基本统计函数如下表所述。
| Sr. No. | 功能说明 |
|---|---|
| 1 | describe() 计算传递的数组的几个描述性统计信息 |
| 2 | gmean() 计算沿指定轴的几何平均值 |
| 3 | hmean() 计算沿指定轴的调和平均值 |
| 4 | kurtosis() 计算峰度 |
| 5 | mode() 返回模态值 |
| 6 | skew() 测试数据的偏差 |
| 7 | f_oneway() 执行单因子方差分析 |
| 8 | iqr() 计算沿指定轴的数据的四分位数范围 |
| 9 | zscore() 计算样本中每个值的z得分,相对于样本均值和标准差 |
| 10 | sem() 计算输入数组中值的平均值(或标准测量误差)的标准误差 |
其中一些函数在scipy.stats.mstats有类似的版本,它们适用于屏蔽数组。 让我们通过下面给出的例子来理解这一点。
from scipy import stats
import numpy as np
x = np.array([1,2,3,4,5,6,7,8,9])
print x.max(),x.min(),x.mean(),x.var()
上述程序将生成以下输出。
(9, 1, 5.0, 6.666666666666667)
T-test
让我们了解T-test在SciPy中是如何有用的。
ttest_1samp
计算一组分数的平均值的T检验。 这是对零假设的双边检验,即独立观察样本'a'的预期值(平均值)等于给定的总体平均值, popmean 。 让我们考虑以下示例。
from scipy import stats
rvs = stats.norm.rvs(loc = 5, scale = 10, size = (50,2))
print stats.ttest_1samp(rvs,5.0)
上述程序将生成以下输出。
Ttest_1sampResult(statistic = array([-1.40184894, 2.70158009]),
pvalue = array([ 0.16726344, 0.00945234]))
比较两个样本
在以下示例中,有两个样本,可以来自相同或不同的分布,我们想测试这些样本是否具有相同的统计属性。
ttest_ind - 计算两个独立分数样本均值的T检验。 这是零假设的双侧检验,即两个独立样本具有相同的平均(预期)值。 该测试假设群体默认具有相同的方差。
如果我们观察来自相同或不同群体的两个独立样本,我们可以使用该测试。 让我们考虑以下示例。
from scipy import stats
rvs1 = stats.norm.rvs(loc = 5,scale = 10,size = 500)
rvs2 = stats.norm.rvs(loc = 5,scale = 10,size = 500)
print stats.ttest_ind(rvs1,rvs2)
上述程序将生成以下输出。
Ttest_indResult(statistic = -0.67406312233650278, pvalue = 0.50042727502272966)
您可以使用相同长度的新数组进行相同的测试,但具有不同的平均值。 在loc使用不同的值并测试相同的值。
SciPy - CSGraph
CSGraph代表Compressed Sparse Graph ,它专注于基于稀疏矩阵表示的快速图算法。
图形表示
首先,让我们了解稀疏图是什么以及它在图表表示中的作用。
什么是稀疏图?
图只是节点的集合,它们之间有链接。 图表几乎可以代表任何东西 - 社交网络连接,其中每个节点都是一个人并且与熟人相连; 图像,其中每个节点是像素并且连接到相邻像素; 高维分布中的点,每个节点连接到最近的邻居; 几乎任何你能想象到的东西。
表示图数据的一种非常有效的方法是在稀疏矩阵中:让我们称之为G.矩阵G的大小为N×N,G [i,j]给出节点'i'和节点之间的连接值'J'。 稀疏图形主要包含零 - 也就是说,大多数节点只有少量连接。 在大多数感兴趣的情况下,该属性证明是正确的。
稀疏图子模块的创建是由scikit-learn中使用的几种算法推动的,其中包括以下内容 -
Isomap - 一种流形学习算法,需要在图形中找到最短路径。
Hierarchical clustering - 一种基于最小生成树的聚类算法。
Spectral Decomposition - 一种基于稀疏图拉普拉斯算子的投影算法。
作为一个具体的例子,假设我们想要代表以下无向图 -

该图有三个节点,其中节点0和1通过权重2的边连接,节点0和2通过权重1的边连接。我们可以构造密集,掩蔽和稀疏表示,如下例所示,请记住,无向图由对称矩阵表示。
G_dense = np.array([ [0, 2, 1],
[2, 0, 0],
[1, 0, 0] ])
G_masked = np.ma.masked_values(G_dense, 0)
from scipy.sparse import csr_matrix
G_sparse = csr_matrix(G_dense)
print G_sparse.data
上述程序将生成以下输出。
array([2, 1, 2, 1])
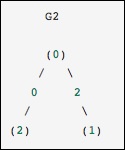
这与前面的图相同,除了节点0和2通过零权重边连接。 在这种情况下,上面的密集表示会导致歧义 - 如果零是有意义的值,如何表示非边缘。 在这种情况下,必须使用掩码或稀疏表示来消除歧义。
让我们考虑以下示例。
from scipy.sparse.csgraph import csgraph_from_dense
G2_data = np.array
([
[np.inf, 2, 0 ],
[2, np.inf, np.inf],
[0, np.inf, np.inf]
])
G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf)
print G2_sparse.data
上述程序将生成以下输出。
array([ 2., 0., 2., 0.])
使用稀疏图表的字梯子
Word Ladders是由Lewis Carroll发明的游戏,通过在每一步更改单个字母来链接单词。 例如 -
APE → APT → AIT → BIT → BIG → BAG → MAG → MAN
在这里,我们分七步从“APE”变为“MAN”,每次更换一个字母。 问题是 - 我们可以使用相同的规则找到这些单词之间的较短路径吗? 这个问题自然表示为稀疏图问题。 节点将对应于单个单词,并且我们将在最多相同的单词之间创建连接 - 一个字母。
获得单词列表
首先,当然,我们必须获得有效单词列表。 我正在运行Mac,而Mac在以下代码块中给出的位置有一个单词字典。 如果您使用的是其他体系结构,则可能需要搜索一下才能找到系统字典。
wordlist = open('/usr/share/dict/words').read().split()
print len(wordlist)
上述程序将生成以下输出。
235886
我们现在想看看长度为3的单词,所以让我们选择正确长度的单词。 我们还将消除以大写字母(专有名词)开头或包含非字母数字字符(如撇号和连字符)的单词。 最后,我们将确保所有内容都是小写的,以便稍后进行比较。
word_list = [word for word in word_list if len(word) == 3]
word_list = [word for word in word_list if word[0].islower()]
word_list = [word for word in word_list if word.isalpha()]
word_list = map(str.lower, word_list)
print len(word_list)
上述程序将生成以下输出。
1135
现在,我们列出了1135个有效的三个字母单词(确切的数字可能会根据使用的特定列表而改变)。 这些单词中的每一个都将成为我们图表中的一个节点,我们将创建连接与每对单词相关联的节点的边,这两个单词仅相差一个字母。
import numpy as np
word_list = np.asarray(word_list)
word_list.dtype
word_list.sort()
word_bytes = np.ndarray((word_list.size, word_list.itemsize),
dtype = 'int8',
buffer = word_list.data)
print word_bytes.shape
上述程序将生成以下输出。
(1135, 3)
我们将使用每个点之间的汉明距离来确定哪些词对是连接的。 汉明距离测量两个向量之间的条目部分,它们不同:汉明距离等于1/N1/N的任何两个单词,其中NN是字梯数,它们连接在单词梯形图中。
from scipy.spatial.distance import pdist, squareform
from scipy.sparse import csr_matrix
hamming_dist = pdist(word_bytes, metric = 'hamming')
graph = csr_matrix(squareform(hamming_dist < 1.5/word_list.itemsize))
比较距离时,我们不使用相等,因为浮点值可能不稳定。 只要单词列表的两个条目不相同,不等式就会产生所需的结果。 现在,我们的图形已经设置好,我们将使用最短路径搜索来查找图形中任意两个单词之间的路径。
i1 = word_list.searchsorted('ape')
i2 = word_list.searchsorted('man')
print word_list[i1],word_list[i2]
上述程序将生成以下输出。
ape, man
我们需要检查这些是否匹配,因为如果单词不在列表中,则输出中将出现错误。 现在,我们所需要的只是在图中找到这两个指数之间的最短路径。 我们将使用dijkstra’s算法,因为它允许我们只找到一个节点的路径。
from scipy.sparse.csgraph import dijkstra
distances, predecessors = dijkstra(graph, indices = i1, return_predecessors = True)
print distances[i2]
上述程序将生成以下输出。
5.0
因此,我们看到'ape'和'man'之间的最短路径只包含五个步骤。 我们可以使用算法返回的前驱来重构此路径。
path = []
i = i2
while i != i1:
path.append(word_list[i])
i = predecessors[i]
path.append(word_list[i1])
print path[::-1]i2]
上述程序将生成以下输出。
['ape', 'ope', 'opt', 'oat', 'mat', 'man']
SciPy - Spatial
scipy.spatial package可以通过利用Qhull library来计算一组点的Triangulations,Voronoi Diagrams和Convex Qhull library 。 此外,它包含用于最近邻点查询的KDTree implementations以及用于各种度量中的距离计算的实用程序。
Delaunay三角测量
让我们了解Delaunay Triangulations是什么以及它们如何在SciPy中使用。
什么是Delaunay三角测量?
在数学和计算几何中,对于给定的平面中的离散点集合P的Delaunay三角剖分是三角测量DT(P) ,使得DT(P)中没有点在DT(P)中的任何三角形的外接圆内。
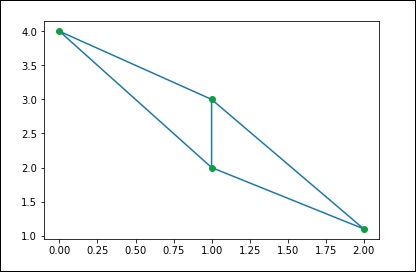
我们可以通过SciPy进行相同的计算。 让我们考虑以下示例。
from scipy.spatial import Delaunay
points = np.array([[0, 4], [2, 1.1], [1, 3], [1, 2]])
tri = Delaunay(points)
import matplotlib.pyplot as plt
plt.triplot(points[:,0], points[:,1], tri.simplices.copy())
plt.plot(points[:,0], points[:,1], 'o')
plt.show()
上述程序将生成以下输出。
共面点数
让我们了解共面点是什么以及如何在SciPy中使用它们。
什么是共面点数?
共面点是位于同一平面内的三个或更多点。 回想一下,平面是一个平面,在所有方向上都没有尽头延伸。 它通常在数学教科书中显示为四面图。
让我们看看如何使用SciPy找到它。 让我们考虑以下示例。
from scipy.spatial import Delaunay
points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
tri = Delaunay(points)
print tri.coplanar
上述程序将生成以下输出。
array([[4, 0, 3]], dtype = int32)
这意味着点4位于三角形0和顶点3附近,但不包括在三角测量中。
凸壳
让我们了解凸壳是什么以及如何在SciPy中使用它们。
什么是Convex Hulls?
在数学中,欧几里得平面或欧几里德空间(或更一般地,在实数上的仿射空间中)的一组点X的convex hull或convex envelope是包含X的最小convex set 。
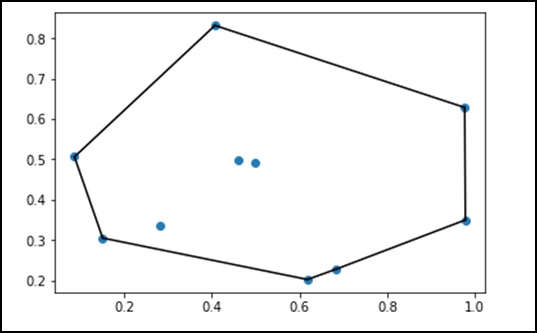
让我们考虑以下示例来详细了解它。
from scipy.spatial import ConvexHull
points = np.random.rand(10, 2) # 30 random points in 2-D
hull = ConvexHull(points)
import matplotlib.pyplot as plt
plt.plot(points[:,0], points[:,1], 'o')
for simplex in hull.simplices:
plt.plot(points[simplex,0], points[simplex,1], 'k-')
plt.show()
上述程序将生成以下输出。
SciPy - ODR
ODR代表Orthogonal Distance Regression ,用于回归研究。 基本线性回归通常用于通过绘制图表上的最佳拟合线来估计两个变量y和x之间的关系。
用于此的数学方法称为Least Squares ,旨在最小化每个点的平方误差之和。 这里的关键问题是如何计算每个点的误差(也称为残差)?
在标准线性回归中,目标是从X值预测Y值 - 因此明智的做法是计算Y值中的误差(如下图中的灰线所示)。 但是,有时考虑X和Y中的误差更为明智(如下图中红色虚线所示)。
例如 - 当您知道X的测量值不确定时,或者您不想关注一个变量的误差而不是另一个变量的误差时。
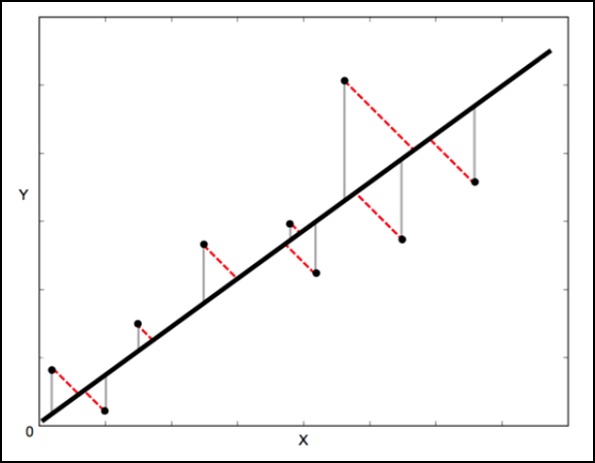
正交距离回归(ODR)是一种可以做到这一点的方法(在这种情况下正交意味着垂直 - 所以它计算垂直于线的误差,而不仅仅是'垂直')。
scipy.odr单变量回归的实现
以下示例演示了单变量回归的scipy.odr实现。
import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import *
import random
# Initiate some data, giving some randomness using random.random().
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([i**2 + random.random() for i in x])
# Define a function (quadratic in our case) to fit the data with.
def linear_func(p, x):
m, c = p
return m*x + c
# Create a model for fitting.
linear_model = Model(linear_func)
# Create a RealData object using our initiated data from above.
data = RealData(x, y)
# Set up ODR with the model and data.
odr = ODR(data, linear_model, beta0=[0., 1.])
# Run the regression.
out = odr.run()
# Use the in-built pprint method to give us results.
out.pprint()
上述程序将生成以下输出。
Beta: [ 5.51846098 -4.25744878]
Beta Std Error: [ 0.7786442 2.33126407]
Beta Covariance: [
[ 1.93150969 -4.82877433]
[ -4.82877433 17.31417201
]]
Residual Variance: 0.313892697582
Inverse Condition #: 0.146618499389
Reason(s) for Halting:
Sum of squares convergence
SciPy - Special Package
特殊包中可用的功能是通用功能,它遵循广播和自动阵列循环。
让我们看看一些最常用的特殊功能 -
- 立方根函数
- 指数函数
- 相对误差指数函数
- 对数和指数函数
- 兰伯特函数
- 排列和组合功能
- 伽玛功能
现在让我们简要地了解这些功能。
立方根函数
此立方根函数的语法是 - scipy.special.cbrt(x)。 这将获取x逐元素立方根。
让我们考虑以下示例。
from scipy.special import cbrt
res = cbrt([10, 9, 0.1254, 234])
print res
上述程序将生成以下输出。
[ 2.15443469 2.08008382 0.50053277 6.16224015]
指数函数
指数函数的语法是 - scipy.special.exp10(x)。 这将计算10 ** x元素。
让我们考虑以下示例。
from scipy.special import exp10
res = exp10([2, 9])
print res
上述程序将生成以下输出。
[1.00000000e+02 1.00000000e+09]
相对误差指数函数
此函数的语法是 - scipy.special.exprel(x)。 它生成相对误差指数,(exp(x) - 1)/ x。
当x接近零时,exp(x)接近1,因此exp(x)-1的数值计算可能遭受灾难性的精度损失。 然后实现exprel(x)以避免精度损失,这在x接近零时发生。
让我们考虑以下示例。
from scipy.special import exprel
res = exprel([-0.25, -0.1, 0, 0.1, 0.25])
print res
上述程序将生成以下输出。
[0.88479687 0.95162582 1. 1.05170918 1.13610167]
对数和指数函数
该函数的语法是 - scipy.special.logsumexp(x)。 它有助于计算输入元素的指数总和的对数。
让我们考虑以下示例。
from scipy.special import logsumexp
import numpy as np
a = np.arange(10)
res = logsumexp(a)
print res
上述程序将生成以下输出。
9.45862974443
兰伯特函数
此函数的语法是 - scipy.special.lambertw(x)。 它也被称为Lambert W函数。 Lambert W函数W(z)被定义为w * exp(w)的反函数。 换句话说,对于任何复数z,W(z)的值使得z = W(z)* exp(W(z))。
Lambert W函数是一个具有无限多个分支的多值函数。 每个分支给出方程z = w exp(w)的单独解。 这里,分支由整数k索引。
让我们考虑以下示例。 这里,Lambert W函数是w exp(w)的倒数。
from scipy.special import lambertw
w = lambertw(1)
print w
print w * np.exp(w)
上述程序将生成以下输出。
(0.56714329041+0j)
(1+0j)
排列和组合
让我们分别讨论排列和组合,以便清楚地理解它们。
Combinations - 组合函数的语法是 - scipy.special.comb(N,k)。 让我们考虑以下示例 -
from scipy.special import comb
res = comb(10, 3, exact = False,repetition=True)
print res
上述程序将生成以下输出。
220.0
Note - 仅对exact = False大小写接受数组参数。 如果k“N,N”0或k“0,则返回0。
Permutations - 组合函数的语法是 - scipy.special.perm(N,k)。 N个事物的排列一次取k,即N的k-排列。这也称为“部分排列”。
让我们考虑以下示例。
from scipy.special import perm
res = perm(10, 3, exact = True)
print res
上述程序将生成以下输出。
720
伽玛功能
对于自然数'n',伽马函数通常被称为广义阶乘,因为z * gamma(z)= gamma(z + 1)和gamma(n + 1)= n !,
组合函数的语法是 - scipy.special.gamma(x)。 N个事物的排列一次取k,即N的k-排列。这也称为“部分排列”。
组合函数的语法是 - scipy.special.gamma(x)。 N个事物的排列一次取k,即N的k-排列。这也称为“部分排列”。
from scipy.special import gamma
res = gamma([0, 0.5, 1, 5])
print res
上述程序将生成以下输出。
[inf 1.77245385 1. 24.]
